--%>
Assignment Help - homework help

State Prime number theorem

Prime number theorem: A big deal is known about the distribution of prime numbers and of the prime factors of a typical number. Most of the mathematics, although, is deep: while the results are often not too hard to state, the proofs are often difficult. We will introduce one fundamental and extremely significant theorem about the distribution of prime numbers. (Its proof is one of the difficult ones!)

Let x be any positive number. We denote by Π (x) the number of prime numbers less than or equal to x. The prime number theorem was conjectured by Gauss in the year 1791 (at the age of 14!), but was not proved until 1896, when it was proved independently through Jacques Hadamard and Charles de la Vallee Poussin.

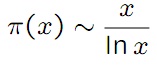
982_prime number.jpg

(Remember that ln x denotes the natural logarithm of x: ln x = loge x.)

   Related Questions in Mathematics

  • Q : Who independently developed

    Who independently developed a model for simply pricing risky assets?

    		•
  • Q : State Prime number theorem Prime number

    Prime number theorem: A big deal is known about the distribution of prime numbers and of the prime factors of a typical number. Most of the mathematics, although, is deep: while the results are often not too hard to state, the proofs are often diffic

    		•
  • Q : Maths assignment complete assignment

    complete assignment with clear solution and explanation

    		•
  • Q : What is the probability that the film

    T.C.Fox, marketing director for Metro-Goldmine Motion Pictures, believes that the studio's upcoming release has a 60 percent chance of being a hit, a 25 percent chance of being a moderate success, and a 15 percent chance of being a flop. To test the accuracy of his op

    		•
  • Q : Set Theory & Model of a Boolean Algebra

    II. Prove that Set Theory is a Model of a Boolean Algebra The three Boolean operations of Set Theory are the three set operations of union (U), intersection (upside down U), and complement ~.  Addition is set

    		•
  • Q : Uniform scaling what is uniform scaling

    what is uniform scaling in computer graphic

    		•
  • Q : Pig Game Using the PairOfDice class

    Using the PairOfDice class design and implement a class to play a game called Pig. In this game the user competes against the computer. On each turn the player rolls a pair of dice and adds up his or her points. Whoever reaches 100 points first, wins. If a player rolls a 1, he or she loses all point

    		•
  • Q : Formal Logic It's a problem set, they

    It's a problem set, they are attached. it's related to Sider's book which is "Logic to philosophy" I attached the book too. I need it on feb22 but feb23 still work

    		•
  • Q : Who firstly discovered mathematical

    Who firstly discovered mathematical theory for random walks, that rediscovered later by Einstein?

    		•
  • Q : Probability and Stochastic assignment

    Introduction to Probability and Stochastic Assignment 1: 1. Consider an experiment in which one of three boxes containing microchips is chosen at random and a microchip is randomly selected from the box.

    		•