--%>
Assignment Help - homework help

Rotational energy and entropy due to rotational motion.

The entropy due to the rotational motion of the molecules of a gas can be calculated.


Linear molecules: as was pointed out, any rotating molecule has a set of allowed rotational energies. For a linear molecule the allowed rotational energies of a molecule of moment of inertia I are given approximated by

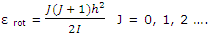
1920_rotational energy.png 

Furthermore, the number of states corresponding to a given value of J is given by 2J + 1. These features of the rotational energy patterns allow the rotational partition function to be deduced. This result can be used to obtain the rotational entropy contribution. The rotational contribution to the entropy, which must be added to the rotational contribution, is given by

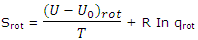
2218_rotational energy1.png 

The partition function for rotation of a linear molecule obtained is

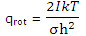
977_rotational energy2.png    

For a linear molecule, which has just 2 rotational degrees of freedom, the value of U - U0 for rotation was found, with this expression, to be RT. The rotational entropy of a diatomic or a linear polyatomic molecule can thus be written

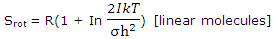
2119_rotational energy3.png 

When numerical values are inserted for the constants, the rotational contributions of linear molecules to the entropy of ideal gases are given by

S°rot (J K-1 mol-1) = 877.37 + 8.3144 (In I + In T - In σ) [I in kg m2]

Example: calculate the 25°C rotational entropy of 1 mol of CO molecules. The moment of inertia of a CO molecule, measured by method given is 14.50 × 10-47 kg m2.

Solution: substitution in eq. and recognizing that σ = 1, gives

S°rot (J K-1 mol-1) = 877.37 + 8.3144[In (14.50 × 10-47) + In 298.15]

= 877.37 + 8.3144 (-105.55 + 5.70)

= 47.17 J K -1 mol-1

For comparison, the translational entropy of 1 mol of CO at 25°C and a pressure of 1 bar is calculated, to be 150.472 J K-1 mol-1.

The much greater translational entropy contribution (compared with the rotational entropy contribution) can be understood in terms of the much closer spacing of the translational energy levels and therefore the much larger number of translational states throughout which the molecules are distributed.

Nonlinear molecules: it is applicable to all diatomic molecules and all linear molecules. Generally shaped molecules, with 3 rather than 2 rotational degrees of freedom, require the use of 3/2 RTfor the rotational energy and the rotational partition function for nonlinear molecules given. For gases composed of such molecules

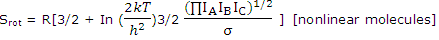
2366_rotational energy4.png 

With numerical values this becomes

S°rot (J K-1 mol-1) = 1320.83 + 4.157 In IAIBIC + 12.471 In T - 8.3143 In σ [IA, IB, IC in kg m2]

Limitations: these equations cannot be applied to molecules with very low moments of inertia or at very low temperatures. In both cases the spacing of the energy levels becomes appreciable compared with the thermal energy, and the integration that produced, for example, is not valid.

   Related Questions in Chemistry

  • Q : Problem on Adiabatic expansion

    Calculate the change in entropy for the system for each of the following cases. Explain the sign that you obtain by a physical argument a) A gas undergoes a reversible, adiabatic expansion from an initial state at 500 K, 1 MPa, and

    		•
  • Q : Concentration of urea Help me to go

    Help me to go through this problem. 6.02x 1020 molecules of urea are present in 100 ml of its solution. The concentration of urea solution is: (a) 0.02 M (b) 0.01 M (c) 0.001 M (d) 0.1 M (Avogadro constant, N4= 6.02x 1023mol -1)<

    		•
  • Q : Examples of reversible reaction

    Describe some examples of a reversible reaction?

    		•
  • Q : Diffusion Molecular View When the

    When the diffusion process is treated as the movement of particles through a solvent the diffusion coefficient can be related to the effective size of diffusing particles and the viscosity of the medium.To see how the experimental coefficients can be treat

    		•
  • Q : Linde liquefaction process Liquefied

    Liquefied natural gas (LNG) is produced using a Linde liquefaction process from pure methane gas at 3 bar and 280 K (conditions at point 1 in figure below). A three-stage compressor with interceding is used to compress the methane to 100 bar (point 2). The first stage

    		•
  • Q : Difference in Mendeleevs table and

    Briefly describe the difference in the Mendeleev’s table and modern periodic table?

    		•
  • Q : Molality of a glucose solution What

    What will be the molality of a solution containing 18g of glucose (having mol. wt. = 180) dissolved in 500g of water: (i) 1m  (ii) 0.5m  (iii) 0.2m  (iv) 2m

    		•
  • Q : Wavelengths which the human eye can see

    Briefly state the wavelengths which the human eye can see?

    		•
  • Q : Reducible Representations The number of

    The number of times each irreducible representation occurs in a reducible representation can be calculated.Consider the C2v point group as described or Appendix C. you can see that (1) sum of

    		•
  • Q : Lab question Explain how dissolving the

    Explain how dissolving the Group IV carbonate precipitate with 6M CH3COOH, followed by the addition of extra acetic acid, establishes a buffer with a pH of approximately 5.

    		•