The absorption of microwave radiation increases the rotational energy of molecules and gives information about the moment of inertia of the molecules.
Now we can begin the study of the spectroscopy that explores the different ways in which the energy of the molecules of a sample can be changed and the use to which the various regions of electromagnetic radiation are put. We begin by investing rotational energy changes-changes that are produced when the molecules of a gas sample absorb far-infrared or microwave radiation.
Rotational energies: the rotational energies of a linear gas-phase molecule were to be given by the expression
εrot = h2/2I J(J + 1) J + 0, 1, 2 .....
And the degeneracies of the rotational levels by gJ = 2J + 1. Since the collections of termsh2/(2I) will occur frequently, it is convenient to introduce the rotational constant B such that
B = h2/2I
Since B is a measure of energy, it will have the units of joules.
In spectroscopy, energies are often expressed in the reciprocal wavelength, or wave number, units of cm-1. The rotational constant in these units is written as B. the rotational energies are then given by
εrot (cm-1) = BJ(J + 1)
Quantities, such as B, expressed in terms of cm-1, can be returned to the SI system by multiplication by c = 2.9979 × 1010 cm and multiplication by h, according to ε = hv. Thus
B(J) = hc?B?
Rotational transitions: the absorption of radiation depends on a nonzero value of the Einstein Blm coefficient. The transition moment for a transition between rotational states of a linear molecule can be expressed by the integration of using the wave functions for the rotational states. (These functions are the angular parts of the wave functions developed to describe the hydrogen atom. An important qualitative result obtained is that the transition moment is nonzero moment is nonzero only if
1. The molecule has a permanent dipole.
2. The transition is between adjacent rotational states: i.e. the change in the rotational quantum number J is given by the "selection rule" ΔJ = ±1. (in transitions in which energy is absorbed, only the ±1 term applies).
The basis for the general rule that only molecules with a dipole can produce rotational spectra can be seen by adopting a classical treatment of the interaction between the radiation and the molecules. Energy can be transferred by a "coupling" of the electric field of the radiation and the dipole of the rotating molecule. The electric field of the radiation can be described by ℘ = ℘ cos 2∏vt. Coupling can occur between the radiation and the molecule if there is a component of the dipole moment of the rotating molecule that is in phase with the radiation electric field. Thus, coupling, and the energy exchange, can be expected if there is dipole moment component with the form
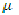(t) = 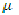cos 2∏vRt, where vR is the rotational frequency of the molecule.
This semiclassical picture shows that energy can be exchanged only if the molecule has a dipole and it suggests a relation between the rotational frequency and the radiation frequency. The quantum mechanical treatment of rotational absorption spectra shows that the frequency relation that applies depends on the energy of the photons of the radiation being equal to the energy needed to produce the ΔJ = ±1 transitions.
Rotational spectra: the far-infrared or microwave absorption spectra of gas samples containing linear polar molecules show regular patterns of nearly equispaced absorption lines. The basis for the relative simplicity of such rotational spectra is now given.
The transitions between rotational energy levels in dipole-based absorption, since the rotational energy levels are closely spaced compared with kT; the molecules will be distributed throughout many of the lower allowed levels. The transitions which can occur are therefore between the many levels, these energy differences correspond to the energies of quantum radiation that bring aboutΔJ ±1 transitions.
We thus expect absorptions of radiation, due to ΔJ = ±1 changes in the rotational energy of the molecules of the sample, to occur at energies given by
Δ εrot = B[(J + 1)(J + 2) - J(J + 1)]
= 2 B(J + 1) J = 0, 1, 2 ....
Or at wave numbers given by
Δ εrot? = v?rot = 2B?(J + 1) J = 0, 1, 2 .....
Thus we expect a pattern of spectral lines corresponding to the wave number values 2B?, 4B?, 6B?. If only a part of such a series is observed, it will show adjacent spectral lines spaced by a constant amount, an amount that can be identified with 2B?.
Molecular dimension: with this analysis we can use the measured spacing between adjacent rotational levels to deduce a value of the rotational constant B? of the molecule. Then with the relation the moment can use the relation I = 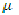r2, where 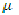is the reduced mass, to obtain a value for the internuclear distance, or bond length, of the molecule.
Example: the average spacing between successive rotational lines is 3.8626 cm-1. Calculate the moment of inertia and the length of the CO bond from this spectral result.
Solution: the reported result is identified with 2B?. Thus
B? = 1.9313 cm-1
And B = (1.9313 cm-1)(2.9979 × 1010 cm s-1)(6.6262 × 10-34 J s)
= 3.836 × 10-23 J
Now we use the relation B = h2/(2I) to obtain
I = h2/2B
= (1.0546 × 10-34 J s)2/2(3.836 × 10-23 J)
= 14.50 × 10-47 kg m2
The reduced mass of C-12 and O-16.CO molecules is obtained from the isotope masses in kilograms and Avogadro's number as
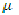= (0.01200)(0.01600)/(0.02800)(6.022 × 1023) = 1.139 × 10-26 kg
Then, with I = 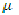r2 we obtain
r2 = 14.50 × 10-47 kg m2/1.139 × 10-26 kg
= 127.3 × 10-22 m2
And r = 112.8 × 10-12 m = 112.8 pm