Explain the mechanism of Enzyme Reactions.

Question

A mechanism for enzyme-catalyzed reactions that leads to the typical rate equation for these reactions can be described.

A variety of rate equations are required to portray the rates of enzymes catalyzed reagents and physical conditions that are encountered. The rate equation of however, is a guide to many of these variations, and the mechanisms of this section, often called the Michaelis-Menten mechanism, is likewise a base for other variations.

The mechanism that accounts for the rate equation is similar to those dealt in with.

With S representing substrate, E the enzyme, and E. S and enzyme substrate complex, the mechanism is presumed to be adequately represented by 

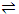E + S  E. S

E. S 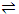 E + products

The steady state assumption, which, however, is not always clearly applicable in these reactions, leads to

k₁[E][S] = k^-1[E. S] + k₂[E. S]

And [E. S] = k₁/k^-1 + k₂ [E][S]

To bring these expressions to a form that can be compared with the empirical rate equation, we must recognize that only [E_tot] = [E] + [E. S], and not [E], is generally known. Often, in fact, only a quantity proportional to [Etot], and not even values of [E_tot], is available.

Replacement of [E] in equation by [E] = [E_tot] - [E. S] leads to

[E. S] = k₁[E_tot][S]/(k^-1 + k₂) + k₁[S]

Now this expression for the intermediate E. S can be inserted into the expression for the rate of the net reaction. This rate can be based on the formation of products in the second mechanism step. We have

-d[S]/dt = R = k₂[E. S] = k₁k₂[E_tot][S]/k^-1 + k₂ + k₁[S]

= k₂[E_tot][S]/k^-1 + k₂)/k₁ + [S]

It is customary for the term (k^-1 + k₂)/k₁ to be obtained by the new symbol K_M, that is,

K_M = k^-1 + k₂/k₁ to give the rate equation result of this mechanism as

R = k₂[E_tot][S]/K_M + [S]

We have come at this stage to the form of the empirical rate equation obtained, we are now in a position to intercept the values of the parameters KM and k₂[E_tot] in terms of their roles in the roles in the steps of the mechanism.

Reference to equation shows that, as the reaction is proceeding

[E][S]/[E. S] = K_M

Thus K_M is related to species concentrations, as is the dissociation equilibrium constant for the species [E. S]. the value of K_M, however, is given by (k...1 + k₂)/k₁, and this equal to the value of the dissociation constant for [E. S] only to the extent that k₂ is small and can be neglected compared with k...1. Thus when the breakup of the E. S complex to form original E and S species dominates the process whereby the complex forms products, the value of KM approaches the dissociation constant for the E. S complex.

What, now, is the significance of the term k₂[E_tot]? One first notes that the rate of the overall reaction is

R = k₂[E. S]

It follows that k₂[E_tot] is the rate that the reaction would have if all the enzyme were in the form of the enzyme-substrate complex. Thus k₂[E_tot] is the maximum rate for a given value of [E_tot]. The turnover rate of an enzyme in a particular enzyme-catalyzed reaction is the rate per mole of enzyme, i.e. the turnover rate is equal to the value of k₂, and this can be calculated fromk₂[Etot] if the total enzyme concentration is known.