Problem on mechanical efficiency of the pump

Question

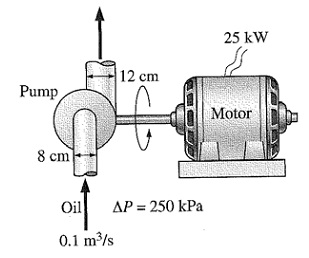
The oil pump is drawing 25 kW of electric power while pumping oil with ρ = 860 kg/m³ at a rate of 0.1 m3/s. The inlet and outlet diameters of the pipe are of 8 cm and 12 cm, respectively. When the pressure rise of oil in the pump is measured to be 250 kPa and the motor efficiency is 90%, then find out the mechanical efficiency of the pump. Taking kinetic energy correction factor to be 1.05.

Answer 1

Given:

Inlet Dia, Di = 8 cm = 8 x 10^-2 m
Outlet Dia, Do = 12cm = 12 x10^-2m

Density of oil,  δ = 80Kg /m³

Flow rate Q = 0.1 m³/s

Pressure rise = 250KPa = 250 x10^-3 Pa

Power supplied to the pump = 25Kw = 25 x 10^-3 w

Motor efficiency = .90

Kinetic energy correction factor, α= 1.05

Inlet area A_i= Π/4 x D₁²=-Π/4 x (8 x 10^-2)² = 0.0804 m²
Outlet area A₀= Π/4 x D₀² = Π/4 x (12 x10^-2)²= 0.1809 m²

Average evolution 
V_i = Q/A_i = 0.1/ 0.804 = 1.1235 m/s
V₀ = Q/A₀ = 0.1/ 0.1809 = 0.5526 m/s

A note of kinetic energy correction factor

K. E correction factor, α = (K. E /See based on actual velocity) / (K. E / See based on average velocity)

The factor α is used when the flow is viscous.

Applying Bernoulli’s equation at the inlet (i) i outlet (0) of the pump.

P_i/ δg + α₁ V_i²/ 2g +z_i + HP= P₀ /δg +α₂ V_o²/2g + Z₀ + Hf .

Given  α_i= α₂= α= 1.05     (Z0 –Zi is considered negligible)
HP = head added by the pump
Hf = head loss due to friction

H= HP – Hf = P₀–P_i / δg + α ( V₀²-V₁²)/ 2g
    = 250 x 10³ / 1000 x 9.81 + 1.05 / 2 x 9.81 (0.55262  - 1.2435)
    = 25.42 m

Power of the pump PP= δg QH
            = 1000 x9.81x 0.1 25.42
            = 24934.85 w
            = 24.934Kw

Mechanical efficiency of the pump:

Case (1)  η_m = power output/power input = 24.934/ 25 = 99%
Case (2)  if the  motor is to get 25Kw  considering its efficiency  the supply should be of 25/ 0.9 KW

η_m = 24.934/ (25/0.9) = 89.67%