Discuss the below:
Fringe Patterns
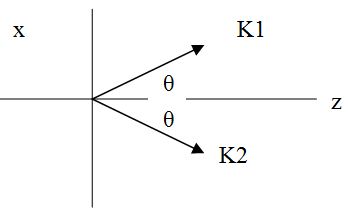
Suppose two mutually coherent plane waves with two different wavelengths, λ1 and λ2, which have corresponding wave number k1 and k2 and corresponding angular frequencies ω1 and ω2. Their wave vectors are confined to the x-z plane and their angles with respect to the z axis are θ1=θ and θ2=-θ as indicated in the figure. The intensity of their interference pattern is given by:
I = I1 +I2 +2√(I1*I2) * cos[(k1-k2)•r - (ω1-ω2)t]
From this, derive the spatial period, Λx, of this fringe pattern in the x direction and temporal period, T. In terms of λ1, λ2, θ1, θ2, and c what is the velocity in the x direction?
Then in terms of λm?λ and θ, derive what condition is necessary for the fringe velocity vx to exceed c, where
λ1 = λm - ?λ and λ2 = λm + ?λ