Problem 1. An investor believes that there will be a big jump in a stock price, but is uncertain as to the direction. Identify six different strategies (spreads or combinations) the investor can follow and explain the differences among them.
Hint: You should also consider the inverse of a spread or combination. For example, the inverse of a spread is called a reverse spread. Relative to a spread, the reverse spread involves 1) a short position where the spread would be a long position and 2) a long position where the spread would be a short position.
Problem 2. Three put options on a stock have the same expiration date and strike prices of $55, $60, and $65. The market prices are $3, $5, and $8, respectively. Explain how a butterfly spread can be created. Construct a table showing the profit from the strategy. For what range of stock prices would the butterfly spread lead to a loss?
|
Stock Price
|
Payoff
|
Profit
|
|
ST < 55
|
|
|
|
55 ≤ ST < 60
|
|
|
|
60 ≤ ST < 65
|
|
|
|
65 ≤ ST
|
|
|
Problem 3. Consider the situation in which stock price movements during the life of a European option are governed by a two-step binomial tree. Explain why it is not possible to set up a position in the stock and the option that remains riskless for the whole of the life of the option.
Problem 4. A stock price is currently $50. It is known that at the end of six months it will be either $60 or $42. The risk-free rate of interest with continuous compounding is 12% per annum. Calculate the value of a six-month European call option on the stock with an exercise price of $48. Verify that no-arbitrage arguments and risk-neutral valuation arguments give the same answers.
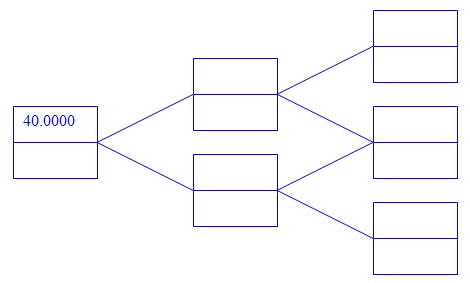
Problem 5. Consider a European call option on a non-dividend-paying stock where the stock price is $40, the strike price is $40, the risk-free rate is 4% per annum, the volatility is 30% per annum, and the time to maturity is six months.
(a) Calculate u, d, a and p for a two-step tree. [Use 4 decimal places in your calculations.]
(b) Value the option using a two-step tree. [Give your final answer to 2 decimal places.]