Differentiation of a single-variable function

Question

Consider the following table of price and quantities produced for a small economy.

a) Assume that all grapes in this economy are used to make wine. Compute nominal GDP for 2000 and 2001.

b) Continue to assume that all grapes are used to make wine. Using 2000 as the base year, compute real GDP in 2000 and 2001.

c) Find the GDP Deflator for 2000 and 2001 on a 100-point scale. Report your answers to two decimal places, if necessary.

d) What was the growth rate for real GDP between 2000 and 2001? Express your answer as a percentage.

e) Assume that the typical consumer in this economy purchases 2 footballs, 1 dress, and 4 bottles of wine per year. Using 2000 as the base year, find the CPI in 2000 and 2001 on a 100-point scale.

f) What was the inflation rate in this economy between 2000 and 2001? Express your answer as a percentage.

Math Review:

1) Differentiation of a Single-Variable Function:

For a function of a single variable: Y = f(X), the derivative of Y with respect to X at a point (X_o) is mathematically defined as :

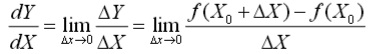
The derivative tells us how will Y change when X changes for an infinitesimally small amount

The derivative of Y with respect to X at the point (Xo) is the slope of the tangent line of the curve Y = f(X) = at the point (X_o) .

For example, let the function C = f(Y) denotes the total cost of producing Y units of output. The derivative of C with respect to Y,(dC/dY), tells us what is the increment of total cost when we increase output by one small amount. This is what we call marginal cost in economics.

Useful rules of differentiation:

(1) The derivative of a constant is zero.

For example, if a cost function only contains fixed cost, such as C = f(Y) = 100; dC/dY = 0

(2) The derivative of Xⁿ with respect to X is X is _nX^n-1 . For example, suppose the cost function takes the form C = Y2 ; dC/dY = 2Y

(3) The derivative of the sum of a finite number of differentiable functions is the sum of their derivatives.

For example, let cost function be C = 100 + 4Y + Y²

(dC/dY) = d(100)/dY + d(4Y)/dY + d(Y2)/dY = 0 + 4 + 2Y = 4 + 2Y

2 Partial Differentiation:

For a function of two variables Z = f(X,Y): The partial derivative of Z = f(X,Y) with respect to X at (Xo, Yo) is just the usual derivative of the function with respect to X holding the value of Y as a constant.

It tells us what the change of Z is when X changes for an infinitesimally small amount, while Y is held fixed. Mathematically, we write

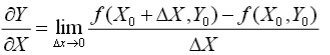
For example, consider Cobb-Douglas production function:

F(K,L) = AK^0.3L^0.3

The marginal product of labor is the partial derivative of th e production function with respect to L .

MPL = ∂F(K,L)/∂L = AK^0.3L^0.7-1 = 0.7AK^0.3L^-0.3

It is the increment of output the firm gets from one extra unit of labor is hired, holding the amount of capital fixed.