Derive an expression for vector using notation of projection

Question

Problem:

Prove the following in several stages:

The composition of any two reflections, whose lines of reflection are orthogonal, is a half-turn.
We will work in the vector space R2

First Stage

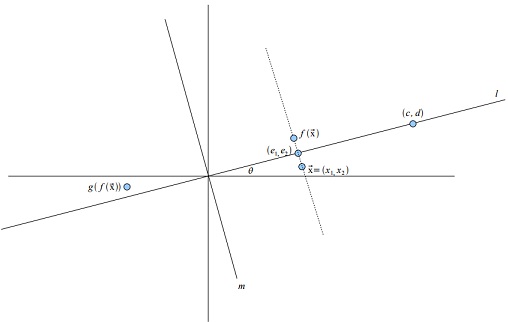
Refer to the diagram provided. The line l makes some angle θ with the x-axis.

Let us suppose that the point (c,d)∈1.(It is clear that, if we were given θ , we could find such a point (c,d) , and if we were given (c,d) , we could find θ .)

Informally, we define f :R²→R² to be the action of reflecting any point x^→ through l .

Now consider any arbitrary x^{→ =}  (x1, x2).(Ignore (e₁, e₂)  in the diagram for now.)

 1. Using the notation of projections, derive an expression for the vector ƒ(x^→)
You may suppose that c is the vector starting at the origin and going to (c,d).
Do not attempt to evaluate it further at this stage; just leave things in terms of c^→ and x^→

Second Stage

 1. Evaluate your expression further, using the formula for the projection of a point. Your final expression must be given in the form  for Ax→ some matrix A  whose entries are in terms of c and d.

Notice that you have constructed a formula for the action of reflecting R 2 through the line going through the origin and (c,d), for any c,d∈ R

Third Stage (sanity check Using your formula, let k∈R and evaluate ƒ((kc,kd)).

 1. What d you get?

Fourth Stage

Consider a specific situation and draw a diagram of it: x^→ =(2,0),(c,d)=(3√(3)).
Take (e1,e2) to be the point of intersection of l and the line orthogonal to l intersecting x^→  .

1. What is θ ?

2. What is (e1, e2)?

You should notice something interesting about the triangle Δ (0,0),(2,0),ƒ((2,0)).

 3 Figure out ƒ((2,0))using standard geometry and this observation.

 4. Now apply your formula to determine ƒ((2,0)). Do you get the same answer?

Fifth Stage

Now rotate your point (c ,d) ninety degrees counterclockwise.

1. What coordinates does it have?

2. Define the line m to be the line through this point and the origin. Define g :R²→ R² to be the action of reflecting points through m . So g(x^→ )=Bx^→,  for some matrix B.
3. According to your formula from the Second Stage, what is B?

Sixth Stage

Now we note that g(ƒ(x^→))=g(Ax^→)=B(Ax^→)(BA)x^→

 1. What is BA? Is this the matrix for the half-turn linear operator?