Sample Questions in Graphical Solution Procedure

Question

Solved problems in Graphical Solution Procedure, sample assignments and homework

Questions: Minimize Z = 10x₁ + 4x₂

Subject to

3x₁ + 2x₂ ≥ 60

            7x₁ + 2x₂ ≥ 84

            3x₁ +6x₂ ≥ 72

x₁ ≥ 0 , x₂ ≥ 0

 

Answer

The first constraint 3x₁ + 2x₂ ≥ 60, can be written in form of equation

3x₁ + 2x₂ = 60

Place x₁ =0, then x₂ = 30

Place x₂ =0, then x₁ = 20

Then the coordinates are (0, 30) and (20, 0)

 

The second constraint 7x₁ + 2x₂ ≥ 84, can be written in form of equation

7x₁ + 2x₂ = 84

Place x₁ =0, then x₂ = 42

Place x₂ =0, then x₁ = 12

The coordinates then are (0, 42) and (12, 0)

 

The third constraint 3x₁ +6x₂ ≥ 72, can be written in form of equation

3x₁ +6x₂ = 72

Place x₁ =0, then x₂ = 12

Place x₂ =0, then x₁ = 24

Thus, coordinates are (0, 12) and (24, 0)

 

The graphical presentation is

 

  

 

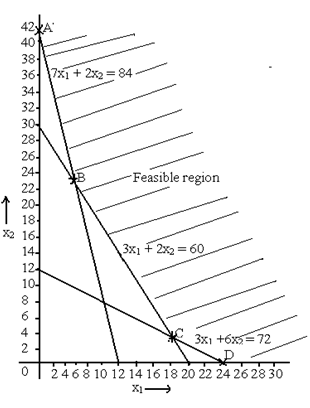
The corner positions of feasible region are A, B, C and D. Thus the coordinates for the corner points are

A (0, 42)

B (6, 21) (Solve the two equations 7x₁ + 2x₂ = 84 and 3x₁ + 2x₂ = 60 to obtain the coordinates)

C (18, 3) Solve the two equations 3x₁ +6x₂ = 72 and 3x₁ + 2x₂ = 60 to obtain the coordinates)

D (24, 0)

 

We are given that Min Z = 10x₁ + 4x₂

At A (0, 42)

Z = 10(0) + 4(42) = 168

 

At B (6, 21)

Z = 10(6) + 4(21) = 144

 

At C (18, 3)

Z = 10(18) + 4(3) = 192

 

At D (24, 0)

Z = 10(24) + 4(0) = 240

 

The minimum value is calculated at the point B. Consequently Min Z = 144 and x₁ = 6, x₂ = 21