Q. What is pure ALOHA and the slotted ALOHA? Consider the delay of both pure ALOHA and slotted ALOHA at low load. Which of the one is less also explain your answer.
Answer:- ALOHA:
In the 1970s, Norman Abramson and his colleagues at the University of Hawaii devised a fresh and elegant technique to solve the channel allocation problem. Their work has been increased by many researchers since then (Abramson, 1985). Even though Abramson's work, called the ALOHA system, used the concept of ground-based radio broadcasting, the basic logic is applicable to any system in which uncoordinated users are challenging for the use of a single shared channel. There are the basic two versions of ALOHA: pure and slotted. They differ with the respect that whether time is spitted into discrete slots into which all frames should fit. Pure ALOHA does not need global time synchronization; slotted ALOHA does need.
Pure ALOHA:
The basic logic of an ALOHA system is straightforward: let users transmit whenever they possess the data to be sent. There will be the collisions, and the colliding frames will be spoiled. Though, due to the feedback property of broadcasting, a sender can all the time find out whether its frame was spoiled by listening to the channel, the same way other users perform the task. With a LAN, the feedback is instant; with a satellite, there is the delay of 270 msec before the sender knows if the transmission was successful or not. If listening while transmitting is not feasible for some reason, acknowledgements are required. If the frame was spoiled, the sender just waits a random amount of time and sends the frame again. The waiting time should be random or the same frames will collide over and over again, in the lockstep. Systems in which the multiple users share a common channel in a way that can lead to conflicts are broadly known as contention systems.
We have prepared the frames all the same length since the throughput of ALOHA systems is maximized by having a uniform frame size rather than by allowing uneven length frames. Whenever two frames try to engage the channel at the same time, there will be a collision and both of them will be garbled. If the first bit of a new frame overlaps with the last bit of a frame almost completed, both frames will be entirely destroyed and both will have to be retransmitted later after random time. The checksum cannot distinguish between a whole loss and a near miss.
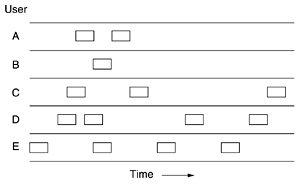
PURE ALOHA
In 1972, Roberts published a technique for doubling the capacity of an ALOHA system (Robert, 1972). His proposal was to split time into discrete intervals, every interval corresponding to one frame. This approach needs the users to agree on slot boundaries.
One way to attain synchronization would be to have one particular station emit a pip at the beginning of each interval, like a clock. In Roberts' technique, which has come to be known as slotted ALOHA, in contrast to Abramson's pure ALOHA, a computer is not allowed to send whenever a carriage return is typed. Instead, it is needed to wait for the starting of the next slot. Therefore the continuous pure ALOHA is made into a discrete one. Since the vulnerable time period is now halved, the possibility of no other traffic during the same slot as our test frame is e-G which leads to the given
Equation
S=Ge-G
As you can see from the Fig.3.3, slotted ALOHA peaks at G = 1, with a throughput of S =1/e or about 0.368, twice that of the pure ALOHA. If this system is operating at G = 1, the probability of a vacant slot is 0.368. The best we can hope for using slotted ALOHA is 37 percent of the slots empty, 37 percent of the successes, and 26 percent of the collisions. Operating at higher values of G decreases the number of empties but raises the number of collisions exponentially.
To see how this quick growth of collisions with G comes about, take the transmission of a test frame. The probability that it will avoid a collision is e-G, the probability that all the other users are quiet in that slot. The probability of a collision then just becomes 1 - e-G. The probability of a transmission desirers exactly k attempts, (i.e., k - 1 collisions followed by the one success).
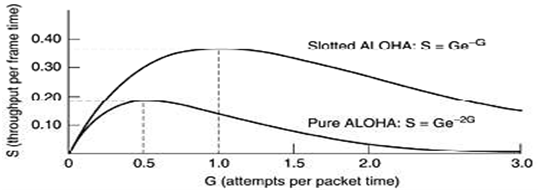
Slotted ALOHA