Quantities in a queuing system

Quantities in a queuing system:

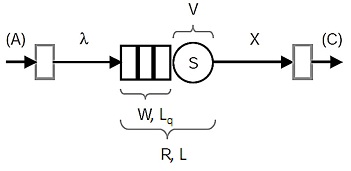
1242_quantities in queuieg.jpg

A: Count of arrivals into system throughout measurement period T

A_k: Count of arrivals into queue k throughout measurement period T

C: Count of global system completions throughout the period T

C_k: Count of completions which departed the queue k during T

V_k: Count of repeated visits to the server k throughout T

λ_k: Arrival rate at resource k = Ak / T

R: Mean time in system (residence time)

L: Average number of requests in system

W: Mean time in queue (that is, waiting time)

L_q: Average number of waiting to be served

S: Mean service time per completed job

X: Throughput

T: Total measurement period or observation time

K: Total number of queuing nodes k in system

View Complete Question

Related Questions in Basic Statistics

Q : Calculate the p- value Medical tests

Medical tests were conducted to learn about drug-resistant tuberculosis. Of 284 cases tested in New Jersey, 18 were found to be drug- resistant. Of 536 cases tested in Texas, 10 were found to be drugresistant. Do these data indicate that New Jersey has a statisti

Q : Computers playing games How Computers

How Computers playing games can be categorized according to different dimensions?

Q : MANOVA and Reflection Activity

Activity 10: MANOVA and Reflection 4Comparison of Multiple Outcome Variables This activity introduces you to a very common technique - MANOVA. MANOVA is simply an extension of an ANOV

Q : What is your conclusion The following

The following data were collected on the number of emergency ambulance calls for an urban county and a rural county in Florida. Is County type independent of the day of the week in receiving the emergency ambulance calls? Use α = 0.005. What is your conclusion? Day of the Week<

Q : State Littles Law Little’s Law : • L =

Little’s Law: • L = λR = XR • Lq = λW = XW • Steady state system • Little’s Law holds as long as customers are not destroyed or&nbs

Q : Statistics for Management Assignment

Q : Hypothesis homework A sample of 9 days

A sample of 9 days over the past six months showed that a clinic treated the following numbers of patients: 24, 26, 21, 17, 16, 23, 27, 18, and 25. If the number of patients seen per day is normally distributed, would an analysis of these sample data provide evidence that the variance in the numbe

Q : State the hypotheses At Western

At Western University the historical mean of scholarship examination score for freshman applications is 900. Population standard deviation is assumed to be known as 180. Each year, the assistant dean uses a sample of applications to determine whether the mean ex

Q : Regression Analysis 1. A planning

1. A planning official in the Texas Department of Community Affairs, which works in the office next to you, has a problem. He has been handed a data set from his boss that includes the costs involved in developing local land use plans for communities wi

Q : Simplified demonstration of Littles Law

Simplified demonstration of Little’s Law:

Discover Q & A

Leading Solution Library

Avail More Than 1435139 Solved problems, classrooms assignments, textbook's solutions, for quick Downloads

No hassle, Instant Access

Start Discovering

18,76,764

1937432
Asked

3,689

Active Tutors

1435139

Questions
Answered

Start Excelling in your courses, Ask an Expert and get answers for your homework and assignments!!

Submit Assignment